Unit 1 - Sig Figs and Measuring Exam Review Answers
1.8: Measurement and Pregnant Figures
- Page ID
- 86583
Learning Objectives
- Identify the number of significant figures in a reported value.
- Utilise the concept of significant figures to limit a measurement to the proper number of digits.
- Recognize the number of significant figures in a given quantity.
The significant figures in a measurement consist of all the certain digits in that measurement plus 1 uncertain or estimated digit. In the ruler illustration below, the bottom ruler gave a length with 2 significant figures, while the top ruler gave a length with 3 significant figures. In a correctly reported measurement, the last digit is significant but non certain. Insignificant digits are not reported. With either ruler, it would not be possible to study the length at \(two.553 \: \text{cm}\) every bit there is no possible way that the thousandths digit could be estimated. The 3 is not meaning and would not exist reported.
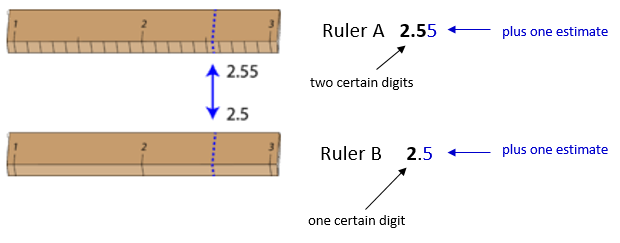
Measurement Uncertainty
Some error or doubt e'er exists in any measurement. The amount of uncertainty depends both upon the skill of the measurer and upon the quality of the measuring tool. While some balances are capable of measuring masses only to the nearest \(0.1 \: \text{g}\), other highly sensitive balances are capable of measuring to the nearest \(0.001 \: \text{g}\) or even better. Many measuring tools such as rulers and graduated cylinders accept small lines which need to be advisedly read in social club to brand a measurement. Effigy \(\PageIndex{1}\) shows two rulers making the same measurement of an object (indicated by the blue arrow).
With either ruler, it is clear that the length of the object is betwixt \(2\) and \(3 \: \text{cm}\). The bottom ruler contains no millimeter markings. With that ruler, the tenths digit tin be estimated and the length may be reported as \(2.5 \: \text{cm}\). Withal, another person may judge that the measurement is \(2.4 \: \text{cm}\) or perhaps \(2.half-dozen \: \text{cm}\). While the 2 is known for certain, the value of the tenths digit is uncertain.
The top ruler contains marks for tenths of a centimeter (millimeters). Now the same object may be measured every bit \(two.55 \: \text{cm}\). The measurer is capable of estimating the hundredths digit because he can exist sure that the tenths digit is a 5. Again, another measurer may report the length to be \(ii.54 \: \text{cm}\) or \(two.56 \: \text{cm}\). In this case, in that location are two certain digits (the 2 and the 5), with the hundredths digit being uncertain. Clearly, the superlative ruler is a superior ruler for measuring lengths as precisely as possible.
Example \(\PageIndex{one}\): Reporting Measurements to the Proper number of Significant Figures
Use each diagram to report a measurement to the proper number of pregnant figures.


Solutions
- The pointer is between 4.0 and 5.0, so the measurement is at least 4.0. The pointer is between the tertiary and fourth modest tick marks, so information technology'southward at to the lowest degree 0.3. We will take to estimate the final place. Information technology looks similar about 1-third of the way across the infinite, so permit united states judge the hundredths identify as iii. Combining the digits, nosotros have a measurement of four.33 psi (psi stands for "pounds per square inch" and is a unit of pressure level, like air in a tire). We say that the measurement is reported to three pregnant figures.
- The rectangle is at to the lowest degree 1.0 cm wide simply certainly not ii.0 cm wide, then the starting time meaning digit is 1. The rectangle's width is past the second tick mark only not the third; if each tick marker represents 0.one, and then the rectangle is at least 0.2 in the next meaning digit. Nosotros have to estimate the next place because there are no markings to guide u.s.a.. Information technology appears to exist about halfway between 0.2 and 0.3, and so we will estimate the next place to be a 5. Thus, the measured width of the rectangle is 1.25 cm. Again, the measurement is reported to three pregnant figures.
Do \(\PageIndex{i}\)
What would exist the reported width of this rectangle?

- Reply
- i.25 cm
When yous look at a reported measurement, it is necessary to be able to count the number of pregnant figures. The rules below details how to determining the number of significant figures in a reported measurement. For the examples, assume that the quantities are correctly reported values of a measured quantity.
Significant Figures Rules
The rules below can be used to determine the number of significant figures reported in a measured number.
Dominion 1: All nonzero digits in a measurement are significant.
- 237 has 3 significant figures.
- 1.897 has four meaning figures.
Dominion two: Zeros that appear between other nonzero digits (i.e., "center zeros") are ever significant.
- 39,004 has five significant figures.
- five.02 has three pregnant figures.
Rule iii: Zeros that announced in front of all of the nonzero digits are called leading zeros. Leading zeros are never significant.
- 0.008 has 1 significant effigy.
- 0.000416 has three pregnant figures.
Dominion 4: Zeros that appear later all nonzero digits are called trailing zeros. A number with trailing zeros that lacks a decimal betoken may or may not be significant.
- 1400 is ambiguous.
- \(1.four \times 10^3\) has two pregnant figures.
- \(1.40 \times 10^three\) 3 meaning figures.
- \(i.400 \times 10^3\) has 4 significant figures.
Dominion v: Abaft zeros in a number with a decimal point are significant. This is true whether the zeros occur earlier or later the decimal point.
- 620.0 has 4 meaning figures.
- nineteen.000 has five significant figures.
Exact Numbers
Integers obtained either by counting objects or from definitions are exact numbers, which are considered to take infinitely many meaning figures. If we have counted 4 objects, for case, and then the number 4 has an infinite number of meaning figures (i.due east., information technology represents 4.000…). Similarly, 1 foot (ft) is defined to comprise 12 inches (in), and so the number 12 in the post-obit equation has infinitely many pregnant figures.
Example \(\PageIndex{ii}\)
Requite the number of significant figures in each. Identify the rule for each.
- 5.87
- 0.031
- 52.90
- 00.2001
- 500
- 6 atoms
Solution
| Caption | Answer |
|---|---|
| a. All iii numbers are significant (dominion 1). | 5.87 , three meaning figures |
| b. The leading zeros are not meaning (rule three). The three and the 1 are meaning (dominion 1) | 0.031, 2 meaning figures |
| c. The 5, the 2 and the 9 are significant (rule 1). The trailing zero is likewise significant (rule 5). | 52.90, 4 significant figures |
| d. The leading zeros are not significant (rule 3). The 2 and the 1 are meaning (rule ane) and the middle zeros are likewise significant (rule two). | 00.2001, four pregnant figures |
| e. The number is cryptic. Information technology could have 1, 2 or three significant figures. | 500, ambiguous |
| f. The half-dozen is a counting number. A counting number is an exact number. | 6, infinite |
Practise \(\PageIndex{2}\)
Give the number of significant figures in each.
- 36.7 m
- 0.006606 due south
- 2,002 kg
- 306,490,000 people
- 3,800 g
- Answer a:
- 3 significant figures.
- Answer b:
- four meaning figures.
- Reply c:
- 4 pregnant figures.
- Answer d:
- Infinite (Exact number)
- Answer e:
- Ambiguous, could exist two, three or four significant figure.
Summary
Uncertainty exists in all measurements. The degree of incertitude is affected in function by the quality of the measuring tool. Significant figures give an indication of the certainty of a measurement. Rules allow decisions to be made about how many digits to use in whatever given state of affairs.
Contributions & Attributions
This page was constructed from content via the following contributor(s) and edited (topically or extensively) by the LibreTexts development team to meet platform style, presentation, and quality:
-
Marisa Alviar-Agnew (Sacramento City College)
-
Henry Agnew (UC Davis)
- Sridhar Budhi
Source: https://chem.libretexts.org/Bookshelves/Introductory_Chemistry/Map:_Fundamentals_of_General_Organic_and_Biological_Chemistry_%28McMurry_et_al.%29/01:_Matter_and_Measurements/1.08:_Measurement_and_Significant_Figures
0 Response to "Unit 1 - Sig Figs and Measuring Exam Review Answers"
Post a Comment